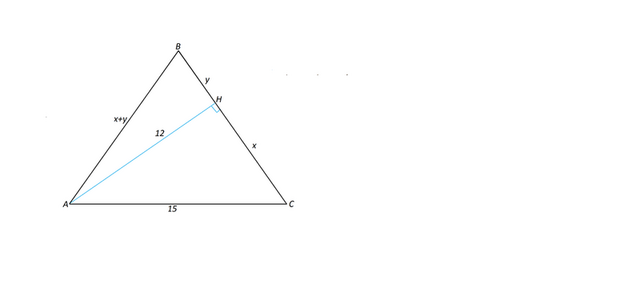
Для решения вспомним т.Пифагора и формулу площади треугольника.
Площадь треугольника находят по формуле:
S=ah:2
Высота
h по условию равна
12.
Сторону ВС, к которой она проведена, нужно найти.
Эта сторона состоит из катетов СН=х и ВН=у двух прямоугольных треугольников.
х² = АС²-АН²
х²=225-144=81
х=√81=9
АВ=ВС=9+у
Из треугольника АВН найдем длину отрезка ВН=у
у²=(9+у)²-12²
у²=81+18у +у²-144
18у=63
у=7/2=3
,5
ВС=9+3
,5=12,5
S (ABC)=AH·ВС:2=12·12,5:2=75(единиц площади)