В равнобедренный треугольник, боковая сторона которого равна 13 и основание 24, вписана окружность. К ней проведена касательная, параллельная основанию. Найдите длину отрезка касательной, ограниченного точками пересечения с боковыми сторонами. (Указание. Докажите подобие треугольников).
Объяснение:
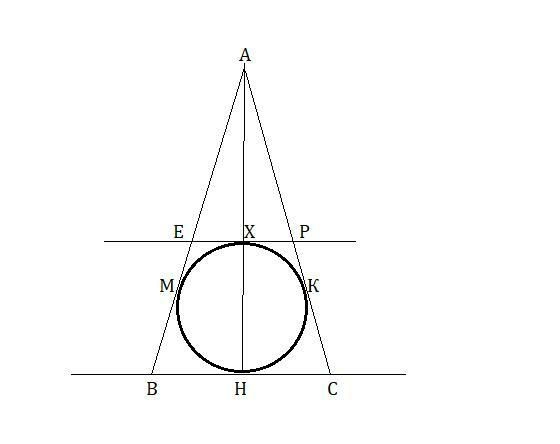
ΔАВС, АВ=АС=13, ВС=24. Отрезок ЕР-отрезкок касательной, ограниченный точками пересечения с боковыми сторонами АВ и АС, ЕР║ВС.
Точки касания расположены В-М-А, С-К-А , В-Н-С.
ΔАЕР подобен ΔАВС по двум углам : ∠А-общий, ∠АЕР=∠АВС как соответственные при ЕР║ВС, АВ-секущая. Отношение периметров равно к . Р(АВС)=26+24=50.
Центр вписанной окружности лежит в точке пересечения биссектрис , а в равнобедренном треугольнике биссектриса АН совпадает с высотой и медианой. Значит ВН=НС=24:2=12 .
АМ=АВ-МВ=АВ-ВН=13-12=1 ⇒ АК=1, тк. треугольник равнобедренный.
По свойству отрезков касательных ЕХ=ЕМ и РХ=РК ⇒Р(АЕР)=2.
к=2/50=1/25.
Тогда ЕР/ВС=1/25 или ЕР=24/25=0,96