Объяснение:

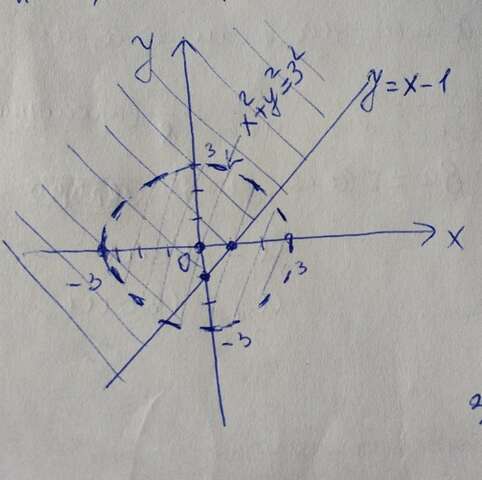
в одной прямоугольной системе координат строим окружность и прямую.
1. уравнение окружности:
 r = 3" alt=" {x}^{2}+{y}^{2}= {r}^{2} \\ {x}^{2} + {y}^{2} = {3}^{2} = > r = 3" align="absmiddle" class="latex-formula">
r = 3" alt=" {x}^{2}+{y}^{2}= {r}^{2} \\ {x}^{2} + {y}^{2} = {3}^{2} = > r = 3" align="absmiddle" class="latex-formula">
решением неравества является "внутренность" окружности, не включая саму окружность( неравенство строгое)
2. прямая у=х-1, находим решение неравенства у>=х-1
прямая у=х-1 " разбивает" плоскость на две полуплоскости.
выберем любую точку, например О(0;0) и подставим её координаты в неравенство, получим
0>=0-1, 0>=-1 (верно), => точка О(0;0) и все точки полуплоскости являются решением неравества у>= х-1
3. решение системы неравенств - часть окружности, ограничения прямой - пересечение штриховок