Ответ:
0
Пошаговое объяснение:
f(x) = 3x^2 - 6x
Находим производную:
f'(x) = 6x - 6
Критические точки:
6x - 6 = 0
x = 1
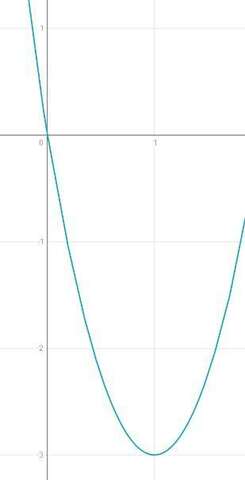
<Если заметить, что наша функция - это парабола, направленная "рогами" вверх (см. чертёж), то тут можно остановиться. Ведь нам сразу известно, что в точке x = 1 функция принимает наименьшее значение. Значит наибольшее на промежутке [0; 1] будет в точке, наиболее удалённой от x = 1, т.е. в точке x = 0. Находим значение f(x) в этой точке и получаем ответ. Но если притвориться, что параболу мы не заметили, то решаем дальше (следующий алгоритм подойдёт для любой функции)>
В этой точке (x = 1) функция f(x) имеет своё наибольшее или наименьшее значение. Найдём это значение.
y = 3 - 6
y = -3
Сравним это значение с другими, чтобы узнать наибольшее оно или наименьшее.
Если x = 0:
y = 3 * 0 - 6 * 0
y = 0
Значит в точке x = 1 функция принимает наименьшее значение. Следовательно, на отрезке [0; 1] наибольшее значение функция примет в точке x = 0. Это значение мы уже нашли (y = 0).