Ответ:
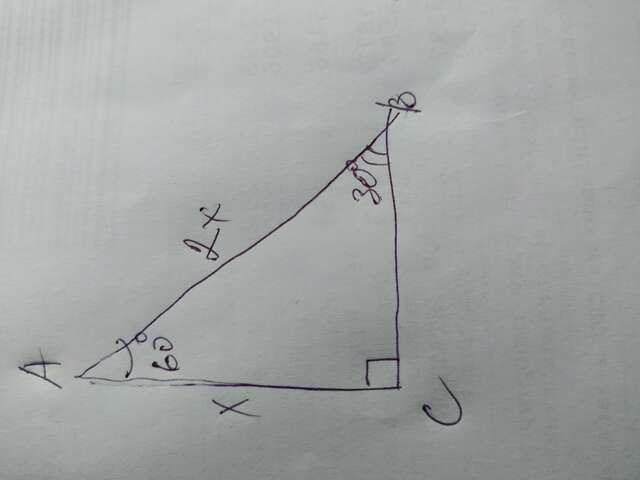
Объяснение: Задание 1
Если в прямоугольном треугольнике один из углов 60° то второй угол будет 30°. Катет, лежащий напротив угла 30°= половине гипотенузы. Пусть катет составляющий с гипотенузой сумму 32,7 будет Х, тогда гипотенуза будет 2х. Составляем уравнение:
х+2х=32,7
3х=32,7
х=10,9
Теперь найдём самую большую сторону, т.е. гипотенузу: гипотенуза= 2х=2х10,9=21,8. Гипотенуза =21,8
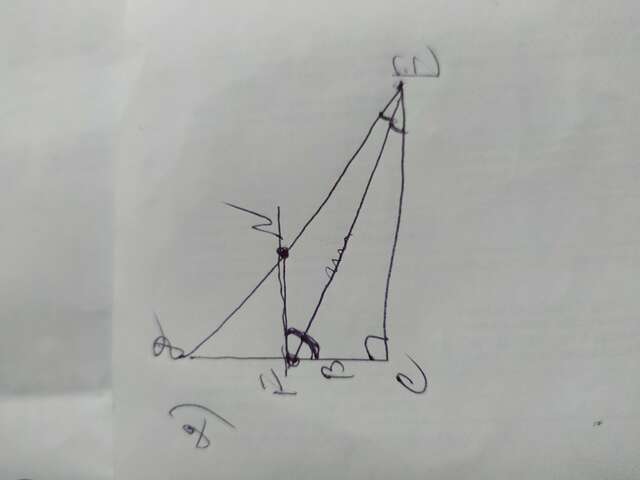
Задание 2
Обозначим расстояние от точки F до прямой DE точкой N, и полученный отрезок будет FN. Рассмотрим треугольники EFN и EFC которые образует биссектриса EF. 1)Сторона EF является общей, 2) угол ENF= углу CEF по условиям, поскольку EF- биссектриса и делит угол пополам; 3) угол NEF = углу EFC=углуEFN как внутренние разносторонние. ∆EFN=∆ EFC по двум углам и стороне между ними. Так как эти треугольники равны, то FC = FN =13
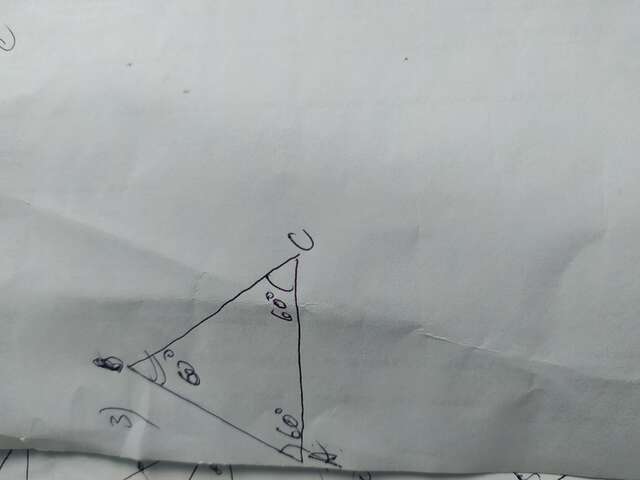
Задание 3
В этом треугольнике углы при основании равны, третий угол будет 180- 60-60=60°. Поэтому все углы в треугольнике равны, и каждый 60° значит он равносторонний.