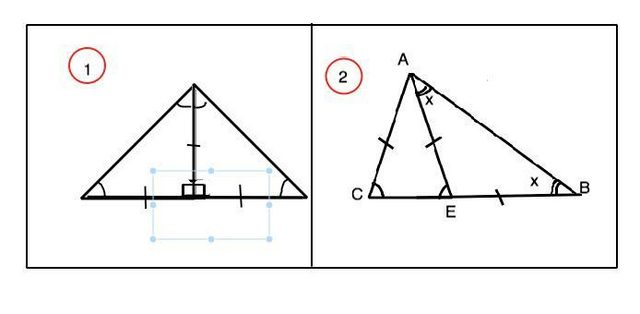
Ответ: 90° и 36°
Объяснение: Очевидно, что для составления из двух равнобедренных треугольников другого, нужно:
- чтобы их боковые стороны были равны;
- чтобы угол одного при составлении дополнял до развернутого угла угол другого (В противном случае получится четырехугольник).
Возможны два варианта решения.
1. Такой треугольник можно составить из равных равнобедренных прямоугольных треугольников Их острые углы равны 45°, и угол между боковым сторонами нового треугольника будет 90°. ( см. рисунок вложения)
2. Обозначим исходные треугольники АВЕ и АСЕ ( АЕ=ВЕ и АЕ=АС). В новом треугольнике АВС АВ=ВС, углы при АС равны. Угол при С общий для обоих треугольников. Треугольники АСЕ и АВС подобны по равным углам при АС. поэтому угол САЕ=углу АВС.
Примем угол АВЕ=ВАЕ= х, тогда угол ВЕА=180°-2х.
=> Смежный с ним угол АЕС=2х, равный ему угол ЕСА=АЕС=2х. В ∆ АВС сумма углов В+А+С=х+2х+2х=180°
5х=180° => х=180°:5=36°