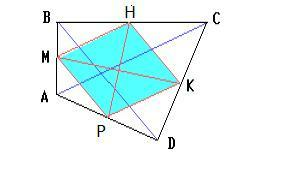
Дано :АВСD-четырехугольник;
М,Н,К ,Р -середины сторон соответственно АВ ВС,СD,ДD.;
МН=НК=КР=РМ .
Доказать :ВD⊥АС.
Объяснение:
По т. о средней линии треугольника ( для ΔАВС и ΔАDС) :
МН||АС и РК ||АС значит МН||РК.
По т. о средней линии треугольника ( для ΔАВD и ΔСВD) : НК||ВD , МР||ВD значит НК||МР.
Поэтому МНКР- параллелограмм. По условию МН=НК=КР=РМ ⇒ параллелограмм является ромбом. А диагонали ромба взаимно перпендикулярны
⇒ВD⊥АС.