Ответ:
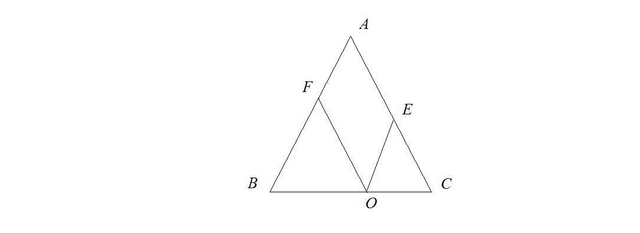
Пусть дан △АВС равнобедренный , ВС - основание, т.О ∈ ВС, F ∈ AB,
E ∈ AC ; ОЕ || АВ и ОF || АС ; ОFАЕ = 32см. Найдём АВ - ?
Решение
∠1 = ∠2 потому что △ АВС равнобедренный ( по условию ).
ОF || АС по условию, поэтому ∠2 =∠3 ( соответственные углы образованные при пересечении этих прямых секущей ВО ), значит
∠1 =∠3.
Рассмотрим △ВFO : равнобедренный, BF = FO.
ОЕ || АВ и ОF || АС по условию,значит OFAE - параллелограмм.
По свойству сторон и углов параллелограмма AF = OE и FO = AE.
Найдём периметр РОFАЕ :
Р(ОFАЕ) = 2 * AF + 2 * FO
Р(ОFАЕ) = 2( AF+FO)
BF = FO , то Р(ОFАЕ) = 2( AF + BF)
Р(ОFАЕ) = 2 * АВ
АВ = Р(ОFАЕ) /2 = 32/2 = 16