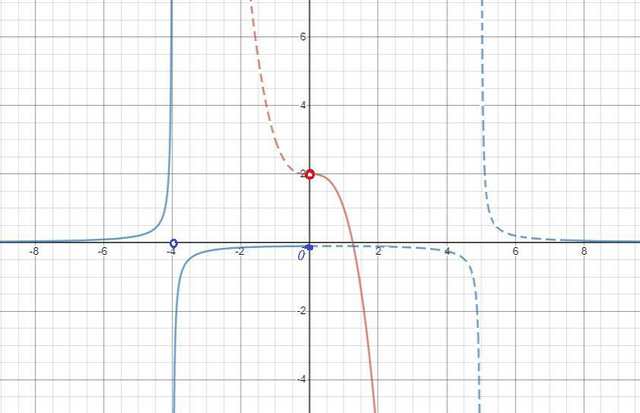
0\; \to \; x\in (0,+\infty )\\\frac{2}{(x-5)(x+4)}\; ,\; \; x\leq 0\; \to \; x\in (-\infty ,0\, ].\end{array}\right\\\\\\y=2-x^3\; \; \to\; \; \; OOF:\; x\in (-\infty ,+\infty )\; \; ;\; \; \underline {(0,+\infty )\in (-\infty ,+\infty )}\\\\y=\frac{2}{(x-5)(x+4)}\; \; \; \to \; \; \; OOF:\; x\ne 5\; ,\; x\ne -4\; ;\; \; \underline {5\notin (-\infty ,0\; ]\; }\; ,\; \underline {-4\in (-\infty ,0\; ]\; }" alt="f(x)=\left\{\begin{array}{l}2-x^3\; ,\; \; \; \; x>0\; \to \; x\in (0,+\infty )\\\frac{2}{(x-5)(x+4)}\; ,\; \; x\leq 0\; \to \; x\in (-\infty ,0\, ].\end{array}\right\\\\\\y=2-x^3\; \; \to\; \; \; OOF:\; x\in (-\infty ,+\infty )\; \; ;\; \; \underline {(0,+\infty )\in (-\infty ,+\infty )}\\\\y=\frac{2}{(x-5)(x+4)}\; \; \; \to \; \; \; OOF:\; x\ne 5\; ,\; x\ne -4\; ;\; \; \underline {5\notin (-\infty ,0\; ]\; }\; ,\; \underline {-4\in (-\infty ,0\; ]\; }" align="absmiddle" class="latex-formula">
0\; \to \; x\in (0,+\infty )\\\frac{2}{(x-5)(x+4)}\; ,\; \; x\leq 0\; \to \; x\in (-\infty ,0\, ].\end{array}\right\\\\\\y=2-x^3\; \; \to\; \; \; OOF:\; x\in (-\infty ,+\infty )\; \; ;\; \; \underline {(0,+\infty )\in (-\infty ,+\infty )}\\\\y=\frac{2}{(x-5)(x+4)}\; \; \; \to \; \; \; OOF:\; x\ne 5\; ,\; x\ne -4\; ;\; \; \underline {5\notin (-\infty ,0\; ]\; }\; ,\; \underline {-4\in (-\infty ,0\; ]\; }" alt="f(x)=\left\{\begin{array}{l}2-x^3\; ,\; \; \; \; x>0\; \to \; x\in (0,+\infty )\\\frac{2}{(x-5)(x+4)}\; ,\; \; x\leq 0\; \to \; x\in (-\infty ,0\, ].\end{array}\right\\\\\\y=2-x^3\; \; \to\; \; \; OOF:\; x\in (-\infty ,+\infty )\; \; ;\; \; \underline {(0,+\infty )\in (-\infty ,+\infty )}\\\\y=\frac{2}{(x-5)(x+4)}\; \; \; \to \; \; \; OOF:\; x\ne 5\; ,\; x\ne -4\; ;\; \; \underline {5\notin (-\infty ,0\; ]\; }\; ,\; \underline {-4\in (-\infty ,0\; ]\; }" align="absmiddle" class="latex-formula">
Для заданной функции ООФ будут действительные значения переменной "х" кроме х= -4, то есть