Ответ:
8/3 кв.ед
Пошаговое объяснение:
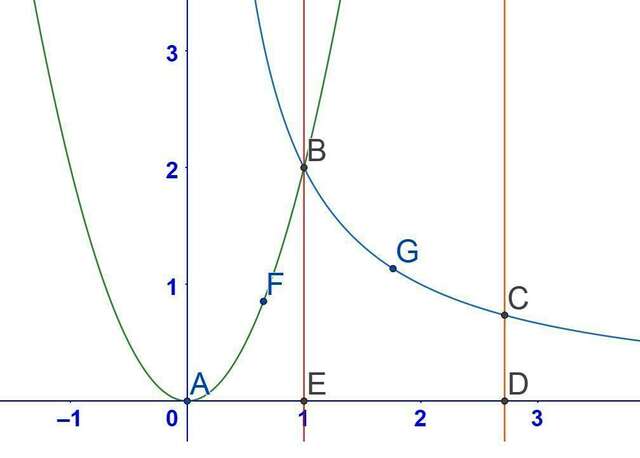
Найдём точки пересечения графиков функций f(x)=2x² и g(x)=2/x
2x²=2/x
2x³=2
x³=1
x=1
Площадь фигуры AFBGCD образованную заданными линиями вычислим как сумму площадей криволинейных трапеций AFBE и BGCDE
F(x)=(2/3)x³+C₁; a=0, b=1
S(AFBE)=F(b)-F(a)=F(1)-F(0)=(2/3)·1³-(2/3)·0³=2/3
G(x)=2ln|x|+C₂, b=1, c=e
S(BGCDE)=G(c)-G(b)=G(e)-G(1)=2lne-2ln1=2·1-2·0=2
S(AFBGCD)=2+2/3=8/3 кв.ед