Ответ:
1. 13 см. 2. Sполн = 108√3см².
Объяснение:
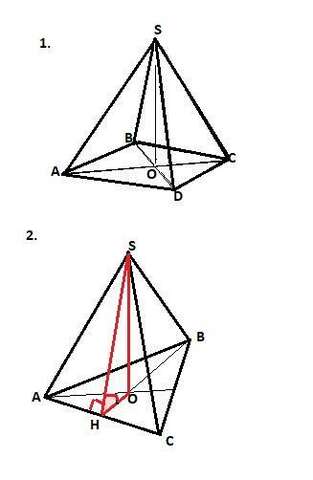
1. Диагонали ромба делятся пополам. Тогда в прямоугольном треугольнике SOC по Пифагору найдем высоту пирамиды SO. SO = √(SC²-OC²) = √(15²-9²) = 12 см.
В прямоугольном треугольнике SOD по Пифагору найдем гипотенузу SD (меньшую боковую грань пирамиды).
SD = √(SO²+OD²) = √(12²+5²) = 13 см.
2. Пирамида правильная => в основании лежит правильный треугольник, а вершина проецируется в центр треугольника (пересечение высот и медиан - в правильном треугольнике это одно и то же). Двугранный угол при стороне основания - это угол между апофемой (высотой грани) и плоскостью основания, то есть это угол SHO. Тогда в прямоугольном треугольнике SHO угол OSH равен 30 градусов (по сумме острых углов треугольника) и гипотенуза SH = 2·OH (по свойству катета, лежащего против угла 30 градусов). По Пифагору 4·ОН² - ОН² = SO². Или 3·ОН² = 36. =>
ОН = 2√3 см. => SH = 4√3 см. ОН - это 1/3 высоты основания. Высота основания ВН = 3·2√3 = 6√3 см. Сторону основания найдем из формулы высоты основания:
h = (√3/2)·h => a = 2h/√3 = 12 см.
Тогда площадь основания пирамиды равна по формуле:
So = (√3/4)·а² = 36√3 cм². Площадь боковой грани (площадь треугольника) равна
Sг = (1/2)·SH·АC = (1/2)·4√3·12 = 24√3 см². Таких граней три. =>
Sбок = 3·24√3 = 72√3 см². Площадь полной поверхности пирамиды равна
S = So+Sбок = 36√3+72√3 = 108√3см².