Задача: Окружность, вписанная в равнобедренный треугольник, делит его боковую сторону на отрезки 5 см и 6 см, начиная от основания. Найти периметр треугольника.
Решение:
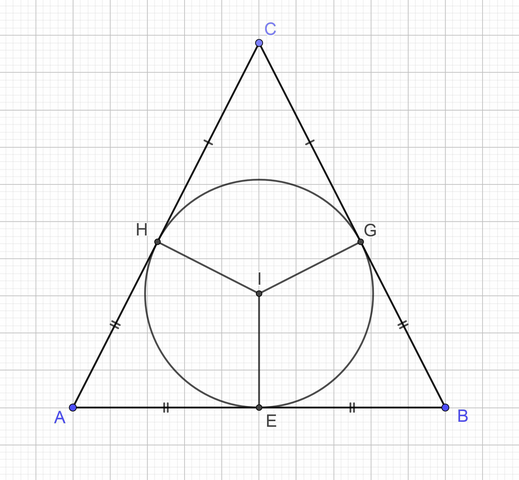
Обозначим треугольник за ABC, AB — основа, AC = BC. Стороны треугольника касаются в точках H,G и E.
Длины касательных к окружности, проведенных с общей точки, равны. Так как ΔABC равнобедренный с основою AB:
CH = CG = 6 см
AH = AE = BG = BE = 5 (см)
AC = BC = AH+CH = 5+6 = 11 (см)
AB = AE+BE = 5+5 = 10 (см)
P = AC+CB+AB = 11·2+10 = 32 (см)
Ответ: Периметр треугольника равен 32 см.