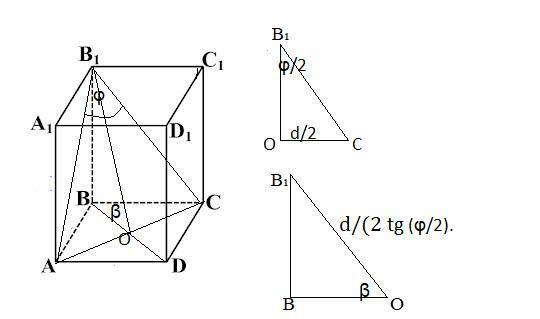
Основой прямой призмы является ромб, меньшая диагональ которого равна d. через эту диагональ и вершину верхнего основания проведена плоскость, которая пересекает плоскости двух соседних боковых граней по прямым, угол между которыми равен φ и образует с плоскостью основания угол β. НАЙДИТЕ ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПРИЗМЫ
Объяснение:
Пусть меньшая диагональ АС=d. Плоскость сечения пересекает плоскости двух соседних боковых граней по прямым В₁А и В₁С, по условию ∠ АВ₁С= φ. Плоскость сечения образует с плоскостью основания угол β. Это угол ∠В₁ОВ , т.к. ОВ⊥АС ( по св. диагоналей ромба) ВВ₁ перпендикуляр к плоскости ⇒ наклонная В₁О⊥АС.
ОС=1/2*d=0,5 d ( по св. диагоналей ромба).
Угол ∠ОВ₁С=φ/2, т.к высота в равнобедренном тр. является биссектрисой.
Δ В₁ОС –прямоугольный : tg (φ/2)=( 0,5 d)/ В₁О, В₁О= d/(2 tg (φ/2).
Δ В₁ВО –прямоугольный : sin β=ВВ₁/ В₁О, ВВ₁= dsin β /(2 tg (φ/2) ;
cos β=ВО/ В₁О , ВО= d/(2 tg (φ/2)* cos β, ВО= d cos β/(2 tg (φ/2).
Δ ОВС- прямоугольный , по т. Пифагора ВС=√ ( ВО²+ОС²),
ВС =d/2 *√ (cos² β/ tg (φ/2)+1)
S(бок. пр.призмы) =Р(осн)*h, h= ВВ₁ , Р(осн)=4*ВС,
Р(осн)=4* d/2 *√ (cos² β/ tg (φ/2)+1)= 2 d√ (cos² β/ tg (φ/2)+1)
S(бок. пр.призмы) = 2 d√ (cos² β/ tg (φ/2)+1)* dsin β /(2 tg (φ/2)=
=2 d² sin β/( √ (cos² β/ tg (φ/2)+1)* tg (φ/2)