Ответ:
а) Смотрим в какой интервал попадает данное нам число. Есть два интервала: х≥-1 и х<-2</p>
Найдем у(3): число 3 - значение по иксу. Смотрим в какому интервалу оно удовлетворяет. 3≥-1 и НЕ 3<-2, значит нам нужно подставить число 3 в первое выражение:</p>
у(3)=3+3=6.
Аналогично проверяем остальные.
у(-4) подходит во второе, подставляем: у(-4)=2*(-4)+2=-8+2=-6.
у(-2) не подходит никуда, соответственно нет значений.
Разберемся с у(√а+3). Корень из отрицательных чисел мы брать не можем, и самих корней отрицательных не бывает, потому выражение в скобках априори будет ≥3, что удовлетворяет первому интервалу, потому подставляем в первое уравнение:
у(а+√3)=√а+3+3=√а+6.
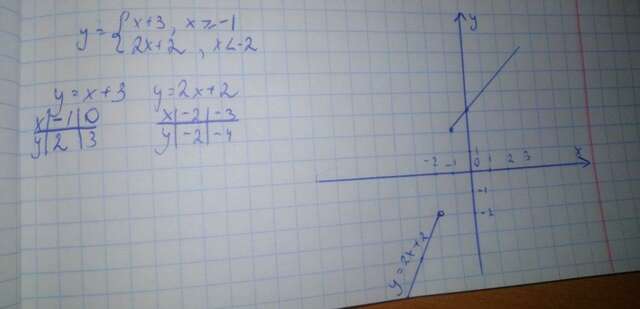
б) См. фото. Объясняю решение: Певрое и второе уравнения - уравнения прямых. Для каждой из них нам дали промежутки, на которых мы должны их построить. Дальше сетка значений, точки, строим. Точка у первой прямой будет закрашена (нестрогое неравенство), а у другой выколота (строгое неравенство).
в) D(y) - область определения функции. По-русски эта штука спрашивает: Какие иксы функции можно брать (существуют)? Смотрим по графику: идем слева направо и на значении -2 у нас выколотая точка, т. е. значение -2 уже брать нельзя, поэтому первая часть области определения: (-∞;-2) (скобка при бесконечности всегда круглая, при -2 зависит от точки: в нашем случае она выколота). Дальше функция пропадает и появляется на значении -1 и продолжается до бесконечности, поэтому вторая часть области определения будет выглядеть так: [-1;+∞). Соберем решение: D(y)=(-∞;-2)∪[-1;+∞)
Е(у) - область значений функции. Она задает тот же вопрос, что и D(y), только эта штука по игрекам. Смотрим по графику: идем снизу вверх и на значении -2 у нас прерывается график, причем в выколотой точке. Первая часть области значений: (-∞;-2). Функция появляется снова на значении 2 и продолжается до бесконечности, вторая часть ответа: [2; +∞). Соберем ответ: E(y)=(-∞;-2)∪ [2; +∞).