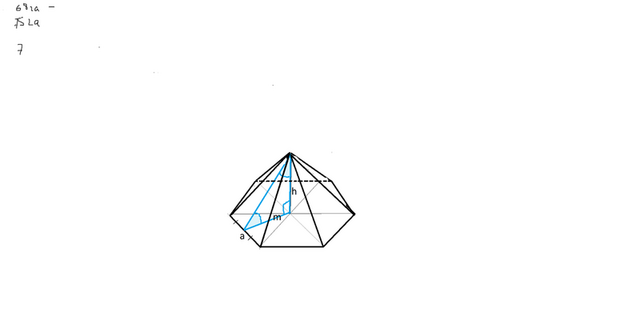
Сторону основания этой пирамиды найдем из ее объема.
Объем пирамиды находят по формуле
V=Sh:3
Площадь основания данной пирамиды - площадь правильного шестиугольника- состоит из суммы площадей шести правильных треугольников.
Пусть сторона каждого из них равна а.
Площадь правильного шестиугольника
S = pr = 3a²√3/2, где p − полупериметр шестиугольникa, a r- радиус вписанной в него окружности, или, иначе - апофема правильного шестиугольника (т.е. высота одного из правильных треугольников, составляющих этот шестиугольник).
Так как боковая грань и основание пирамиды образуют угол 45°, высота пирамиды равна апофеме шестиугольника в основании пирамиды.
Напомню, что апофемой правильного шестиугольника называют перпендикуляр, проведенный из центра к любой стороне. (В задачах редко встречается, но такое название есть).
Высота пирамиды и апофема основаниия здесь - катеты равнобедренного прямоугольного треугольника
m = h= a√3/2
Следовательно,
V={3a²√3):2}·{a√3):2}:3=9a³:12=3a³:4
162=3a³:4
а³=162·4:3=216
а= ∛216=6