Знайдіть площу ромба, сторона якого дорівнює 50 см, а різниця діагоналей

Ответ: 2400 см²

Объяснение:

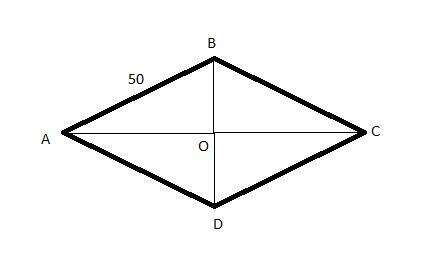
Обозначим большую диагональ AC через x, тогда BD = x - 20.

Т.к. диагонали ромба перпендикулярны и делятся в точке пересечения пополам, то AO = x / 2, BO = x / 2 - 10.

Из прямоугольного ΔAOB по теореме Пифагора:

$AO^{2}+OB^{2}=AB^{2}\\(\frac{x}{2})^{2}+(\frac{x}{2}-10)^{2}=50^{2}\\\frac{x^{2}}{2}-10x+100=2500\\x^{2}-20x-4800=0$

По теореме Виета:

$x_{1}=-60\\x_{2}=80$

Подходит только x = 80.

Площадь ромба равна половине произведения диагоналей:

$S=80*60/2=2400$

Знайдіть площу ромба, сторона якого дорівнює 50 см, а різниця діагоналей – 20 см