Дано: ΔАВD, ∠В = 90º, BD = 8см; ВС – высота; ∠ВАК = 150º. Найти: СD, AС.

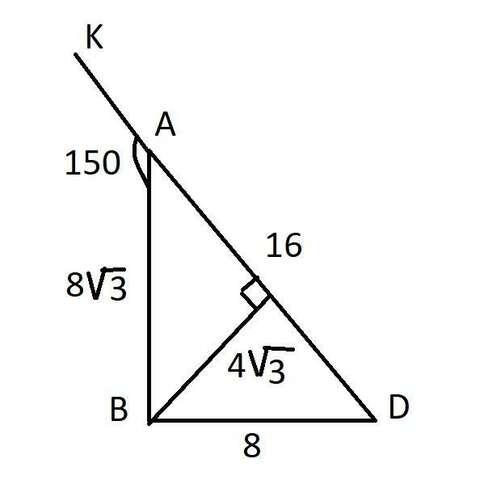
Ответ: CD = 4; AC = 12

Объяснение:

∠A = 30 (Смежные углы)

По свойству катетов AD = 16

Находим по теореме Пифагора сторону BA = $\sqrt{16^{2} - 8^{2}}$ = $8\sqrt{3}$

Находим высоту треугольника BAD; BC= $\frac{8\sqrt{3}* 8 } {16}$ = 4 $\sqrt{3}$

По теореме Пифагора находим сторону СD = $\sqrt{8^{2} - (4\sqrt{3})^{2} }$ = 4

По теореме Пифагора находим сторону AC = $\sqrt{(8\sqrt{3})^{2} - (4\sqrt{3})^{2} }$ = 12