Прямая касается окружности с центром в точке О, в точке В. ** касательной по разные...

Question

Прямая касается окружности с центром в точке О, в точке В. На касательной по разные стороны от точки В отмечены точки К и N такие, что угол BOK = углу ВОN. Найдите угол ОКВ, угол ONB = 56 Помогите пж 20 баллов дам СРОЧНО!!!!!!!!!!!!!!

Answer 1

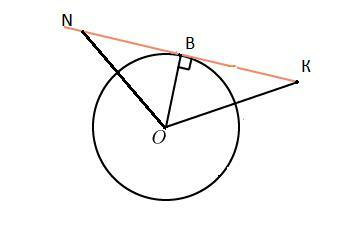
Дано :Окр. О(r) ,ВК-касательная , N∈ВК, ∠BOK=∠ВОN , ∠ONB =56°​ .

Найти ∠ОКВ

Объяснение:

Касательная , проведенная в точку касания, перпендикулярна радиусу ⇒∠NВО =∠КВО=90°

ΔNВО=ΔКВО как прямоугольные по  катету и острому углу  : ВО-общая ,∠BOK=∠ВОN по условию. В равных треугольниках соответственные элементы равны , значит ∠ОNВ=∠ОКВ=56°

---