Знайти площут ромба сторона якого дорівнює 39 см а різниця діагоналей 42 см намалюйте...

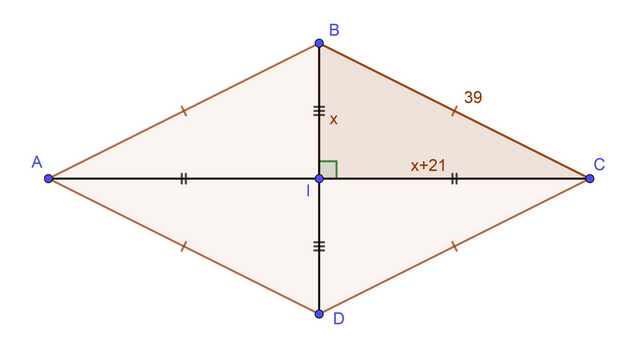
Задача: Найти площадь ромба, сторона которого равна 39 см, а разница диагоналей — 42 см.

Решение:

Точка пересечения диагоналей ромба ABCD делит их на равные отрезки: AI = CI, BI = DI. Диагонали ромба перпендикулярны.

Диагонали делят ромб на 4 равных прямоугольных треугольника с гипотенузой, равной стороне ромба.

Чтобы найти площадь ромба ABCD, достаточно найти площадь одного из образованных треугольников, умножив на 4.

$S_{ABCD}=4S_{\triangle}$

Р-м Δ BCI:

Обозначим стороны треугольника: IB = x (см), CI = x+21 (см), ВС = 39 (см). Применив т. Пифагора, составим и решим уравнение:

$a^2+b^2=c^2\\CI^2+IB^2=BC^2\\(x+21)^2+x^2=39^2\\x^2+42x+441+x^2=1521\\2x^2+42x-1080=0\\x^2+21x-540=0\\D=441+2160=2601=51^2\\x_1=\frac{-21+51}{2} = \frac{30}{2}=15 \\x_2=\frac{-21-51}{2} = \frac{-72}{2}=-36$

0 ≥ x₂ — отбрасываем

IB = x = 15 (см)

CI = x+21 = 15+21 = 36 (см)

Найдем площадь Δ BCI:

$S = \frac{a\cdot b}{2} = \frac{IB\cdot CI}{2} \\S = \frac{15\cdot 36}{2} = \frac{3\cdot 5\cdot 2\cdot 2\cdot 9}{2} =27\cdot 10 = 270 \:\:(cm^2)$

Найдем площадь ромба ABCD:

$S_{ABCD} = 4\cdot S_{\triangle BCI}\\S_{ABCD} = 4\cdot 270 = 1080 \:\: (cm^2)$

Ответ: Площадь ромба равна 1080 см².