(x-2)^2 (x+1)(x-3)

$(x-2)^{2}(x+1)(x-3) < 0$

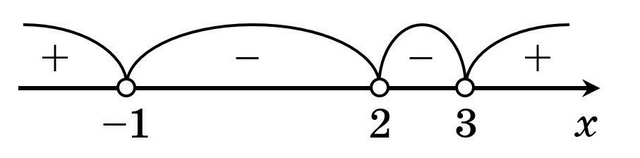
Имеем неравенство высокого порядка. Решим его методом интервалов.

1) Найдем точки пересечения функции $f(x) = (x-2)^{2}(x+1)(x-3)$ с осью абсцисс, приравняв ее к нулю:

$(x-2)^{2}(x+1)(x-3) = 0$

Произведение множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю:

$x - 2 = 0$ , или $x + 1 = 0$ , или $x - 3 = 0$

Тогда $x_{1} = -1; \ x_{2} = 2; \ x_{3} = 3$ — абсциссы точек пересечения функции $f(x)$ с осью абсцисс.

2) Выясним знак (значение) функции $f(x)$ на каждом из четырех участков, подставляя любое значение $x$ из заданного промежутка в функцию (см. вложение).

Следовательно, решением неравенства будет промежуток $x \in (-1; \ 2) \cup (2; \ 3)$

Ответ: $x \in (-1; \ 2) \cup (2; \ 3)$