ПОМОГИТЕ ПОЖАЛУЙСТА, ЗАДАНИЯ ** ФОТО!

Question

Дан 1 ответ

nikebod313_zn · Answer 1 · 2020-06-08T23:20:23+0000

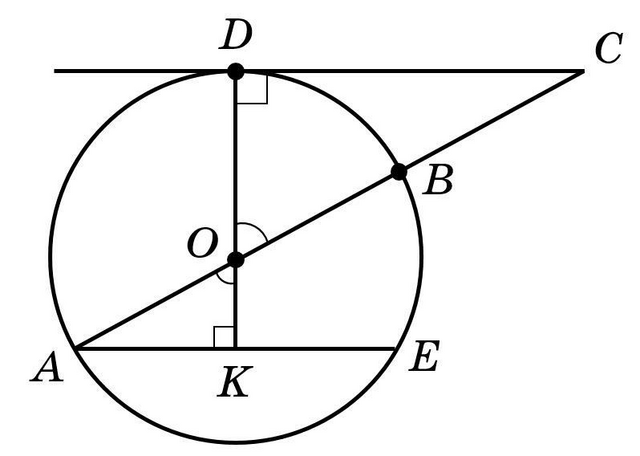
1. Пусть задана окружность с центром в точке $O$ и диаметром $AB = 10$ см. Из точки $C$ , лежащей вне окружности, проведена касательная $CD$ к окружности. $AE$ — отрезок, параллельный $CD$ . $OK = 4$ см — расстояние от точки $O$ до отрезка $AE$ (см. вложение).

Проведем радиус $OD$ к касательной $CD$ , который по свойству окружности будет перпендикулярен ей.

Радиусы $AO = OB = OD = \dfrac{AB}{2} = \dfrac{10}{2} = 5$ см.

$\angle AOK = \angle COD$ как вертикальные.

Треугольники $AOK$ и $COD$ будут подобные (по второму признаку: по двум углам).

Тогда $\dfrac{OK}{OD} = \dfrac{AO}{CO} \Rightarrow CO = \dfrac{OD \cdot AO}{OK} = \dfrac{5 \cdot 5}{4} = \dfrac{25}{4} =6,25$ см.

Ответ: 6,25 см.

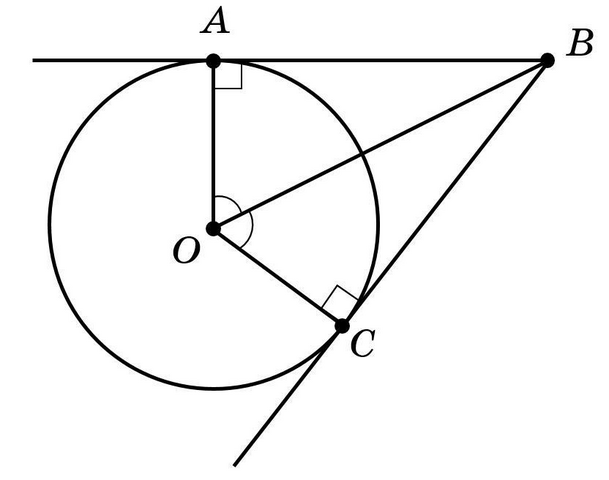
2. Пусть задана окружность с центром в точке $O$ и радиусом $AO = OC = 10$ см. Из точки $B$ , лежащей вне окружности, проведены две касательные $BA$ и $BC$ . Центральный угол $AOC = 60^{\circ}$ (см. вложение).

Радиусы, проведенные к касательным, перпендикулярны им, поэтому $\angle OAB = \angle OCB = 90^{\circ}$

По свойству касательных, проведенных из одной точки, $AB = BC$ .

Тогда отрезок $BO$ разделит четырехугольник $ABCO$ на два равных прямоугольных треугольника: $BAO (\angle A = 90^{\circ})$ и $BCO (\angle C = 90^{\circ})$ , причем $\angle BOA = \angle BOC = \dfrac{\angle AOC}{2} = 30^{\circ}$

Рассмотрим прямоугольный треугольник $BAO$ :

$\cos \angle BOA = \dfrac{AO}{BO}$

$\dfrac{\sqrt{3}}{2} = \dfrac{10}{BO} \Rightarrow BO = \dfrac{2 \cdot 10}{\sqrt{3}} = \dfrac{20 \cdot \sqrt{3}}{\sqrt{3} \cdot \sqrt{3}} = \dfrac{20\sqrt{3}}{3}$

Ответ: $\dfrac{20\sqrt{3}}{3}$

ПОМОГИТЕ ПОЖАЛУЙСТА, ЗАДАНИЯ ** ФОТО!​

ПОМОГИТЕ ПОЖАЛУЙСТА, ЗАДАНИЯ ** ФОТО!