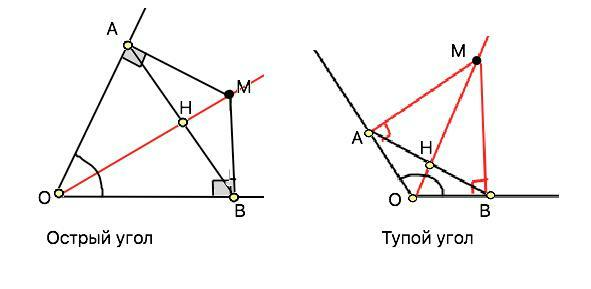
Доказательство для острого и тупого угла одинаково.
По условию ОМ - биссектриса, МА⊥ОА, МВ⊥ОВ =>
Треугольники АОМ и ВОМ прямоугольные, имеют общую гипотенузу ОМ и по равному острому углу ( ∠АОМ=∠ВОМ).
∆ АОМ=∆ ВОМ по 3-му признаку равенства прямоугольных треугольников. . Следовательно, их катеты АО=ВО, поэтому ∆ АОВ - равнобедренный .
В равнобедренном треугольнике биссектриса угла между равными сторонами - еще и медиана и высота.
Высота ОН⊥АВ, ОН принадлежит ОМ. ⇒
АВ⊥ОМ, ч.т.д.