→ Задача №3.
Теорема о неравенстве треугольника звучит следующим образом:
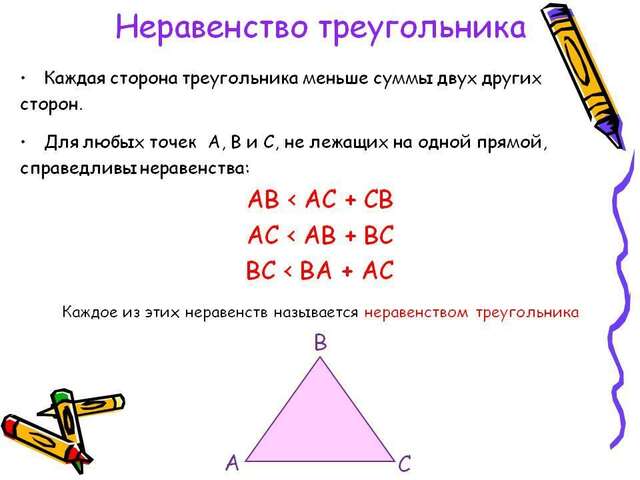
- каждая сторона треугольника меньше суммы двух других сторон.
Соответственно подходит вариант 1) вместо углов должно быть сторон.
Ответ: 1).
→ Задача №4.
Применим теорему о неравенстве треугольника. Для этого нужно сравнить каждую сторону с суммой двух оставшихся сторон.
Треугольник №1:
8 см, 2 см, 9 см.
-
9" alt="8+2>9" align="absmiddle" class="latex-formula"> - верно.
-
8" alt="2+9>8" align="absmiddle" class="latex-formula"> - верно.
-
2" alt="8+9>2" align="absmiddle" class="latex-formula"> - верно.
Значит такой треугольник существует.
Треугольник №2:
18 см, 12 см, 14 см.
-
14" alt="18+12>14" align="absmiddle" class="latex-formula">- верно.
-
12" alt="18+14 >12" align="absmiddle" class="latex-formula"> - верно.
-
18" alt="14+12>18" align="absmiddle" class="latex-formula"> - верно.
Значит такой треугольник существует.
Треугольник №3:
110 см, 100 см, 90 см.
-
90" alt="110+100>90" align="absmiddle" class="latex-formula"> - верно.
-
100" alt="110+90>100" align="absmiddle" class="latex-formula"> - верно.
-
110" alt="90+100>110" align="absmiddle" class="latex-formula"> - верно.
Значит такой треугольник существует.
Треугольник №4:
3 см, 3 см, 7 см.
-
7" alt="3+3>7" align="absmiddle" class="latex-formula"> - неверно.
-
3" alt="3+7>3" align="absmiddle" class="latex-formula"> - верно.
-
3" alt="7+3>3" align="absmiddle" class="latex-formula"> - верно.
Поскольку в первом случае сумма двух сторон меньше другой стороны, то такого треугольника не существует.
Треугольник №5:
79 см, 40 см, 40 см.
-
40" alt="79+40>40" align="absmiddle" class="latex-formula"> - верно.
-
79" alt="40+40>79" align="absmiddle" class="latex-formula"> - верно.
-
40" alt="40+79>40" align="absmiddle" class="latex-formula"> - верно.
Значит такой треугольник существует.
Ответ: 4).
