Задача: Отрезок CP — биссектриса треугольника MKC, ∠MCK = 60°, ∠KPC = 74°. Какова градусная мера угла М?
Решение:
Т.к. СР — биссектриса угла С ⇒ ∠MCP = ∠KCP = 60/2 = 30°.
Внешний угол треугольника равен сумме углов, не смежных с ним ⇒
∠M = ∠KPC−∠MCP° = 74−30 = 44°.
Ответ: градусная мера угла М равна 44°.
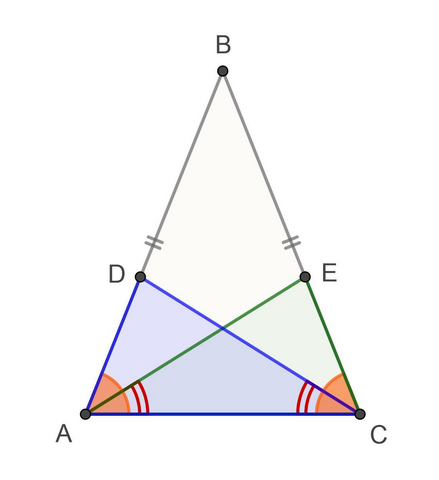
Задача: На боковых сторонах AB и BC равнобедренного треугольника ABC обозначили соответственно точки D и E так, что ∠ACD = ∠CAE. Доказать, что AD = CE.
Доказательство:
Т.к. ΔАВС равнобедренный с основанием АС, ∠BAC = ∠BCA ⇒
⇒ ΔADC = ΔCEA — по стороне и двум прилежащим углам (II признак равенства тр-ков):
- ∠DAC = ∠ECA (∠DAC ∈ ∠BAC) (∠ECA ∈ ∠BCA);
- ∠ACD = ∠CAE — по условию;
- отрезок AC — общий.
Следовательно, из равенства треугольников ΔADC и ΔCEA, AD = CE, что и требовалось доказать.