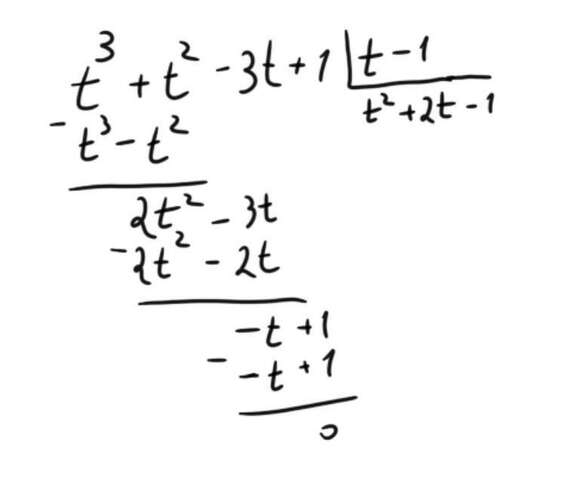Помогите с уравнением!

Question

Дан 1 ответ

QDominus_zn · Answer 1 · 2020-06-08T07:10:08+0000

$\sin(2x) + \sqrt{2} \sin(x - \frac{\pi}{4} ) = 1 \\ \sin(2x) + \sqrt{2} ( \sin(x) \cos( \frac{\pi}{4} ) - \sin( \frac{\pi}{4} ) \cos(x) ) = 1 \\ \sin(2x) + \sqrt{2} \sin(x) \frac{ \sqrt{2} }{2} - \sqrt{2} \frac{ \sqrt{2} }{2} \cos(x) = 1 \\ \sin(2x) + \sin(x) - \cos(x) = 1 \\ 2 \sin(x) \cos(x) + \sin(x) - \cos(x) = 1 \\ \sin(x) = \frac{2 \tan( \frac{x}{2} ) }{1 + \tan {}^{2} ( \frac{x}{2} ) } , \: \cos(x) = \frac{1 - \tan {}^{2} ( \frac{x}{2} ) }{ 1 + \tan {}^{2} ( \frac {x}{2} ) } \\ \tan( \frac{x}{2} ) = t \\ 2 \frac{2t}{1 + {t}^{2} } \frac{1 - {t}^{2} }{1 + {t}^{2} } + \frac{2t}{1 + {t}^{2} } - \frac{1 - {t}^{2} }{1 + {t}^{2} } - 1 = 0 \\ \frac{4t(1 - {t}^{2} ) + 2t(1 + {t}^{2} ) - (1 - {t}^{2} )(1 + {t}^{2} ) - (1 + {t}^{2}) {}^{2} }{(1 + {t}^{2}) {}^{2} } = 0 \\ 4t - 4 {t}^{3} + 2t + 2 {t}^{3} - (1 - ({t}^{2} ) {}^{2} ) -(1 + 2 {t}^{2} + {t}^{4} ) = 0 \\ 6t - 2 {t}^{3} - 1 + {t}^{4} - 1 - 2 {t}^{2} - {t}^{4} = 0 \\ 6t - 2 {t}^{3} - 2 {t}^{2} - 2 = 0 \\ 3t - {t}^{3} - {t}^{2} - 1 = 0 \\ {t}^{3} + {t}^{2} - 3t + 1 = 0$

Легко заметить, что корень t = 1 является корнем данного уравнения относительно t, поэтому воспользуемся теоремой Безу и поделим данный многочлен на одночлен t - 1 (рисунок приложен).

Получили данное следствие:

${t}^{3} + {t}^{2} - 3t + 1 = (t - 1)( {t}^{2} + 2t - 1) = 0 \\ (t - 1)( {t}^{2} + 2t - 1) = 0 \\ \left[ \begin{gathered} t = 1 \\ {t}^{2} + 2t - 1 = 0 \end{gathered} \right.$

Получили первый корень. Подставляем:

$\tan( \frac{x}{2} ) = 1 \\ \frac{x}{2} = \frac{\pi}{4} + \pi n \\ x_{1} = \frac{\pi}{2} + 2\pi n$

Решаем второе уравнение:

${t}^{2} + 2t - 1 = 0 \\ D = {2}^{2} + 4 = 8 \\ \left[ \begin{gathered} t_{1} = \frac{ - 2 + 2 \sqrt{2} }{2} = - 1 + \sqrt{2} \\ t_{2} = \frac{ - 2 - 2 \sqrt{2} }{2} = - 1 - \sqrt{2} \end{gathered} \right.$

Подставляем и находим оставшиеся корни:

$\tan( \frac{x}{2} ) = \sqrt{2} - 1 \\ \frac{x}{2} = \arctg( \sqrt{2} - 1) + \pi n \\ x_{2} = 2 \arctg( \sqrt{2} - 1) + 2\pi n$

$\tan( \frac{x}{2} ) = - 1 - \sqrt{2} \\ \frac{x}{2} = \arctg( - ( \sqrt{2} + 1)) + \pi n \\ x_{3} = - 2 \arctg( \sqrt{2} + 1) + 2\pi n$

Данная подставка накладывает дополнительное условие на х:

$\frac{x}{2} ≠ \frac{\pi}{2} + \pi m \\ x≠\pi + 2\pi m, \: m\in \mathbb Z$

Поэтому необходимо проверить, является ли данное условие корнем уравнения:

$\sin(2x) + \sin(x) - \cos(x) = \sin(2(\pi + 2\pi m)) + \\ + \sin(\pi + 2\pi m) - \cos(\pi + 2\pi m) = 1$

Получили справедливость, поэтому данное условие также является корнем уравнения.

Ответ:

$\left[ \begin{gathered} x_{1} = \frac{\pi}{2} + 2\pi n \\ x_{2} = 2 \arctg( \sqrt{2} - 1) + 2\pi n \\ x_{3} = - 2 \arctg( \sqrt{2} + 1) + 2\pi n \\ x_{4}= \pi + 2\pi n, \: n \in \mathbb Z \end{gathered} \right.$