Ответ:
28,5°
Объяснение:
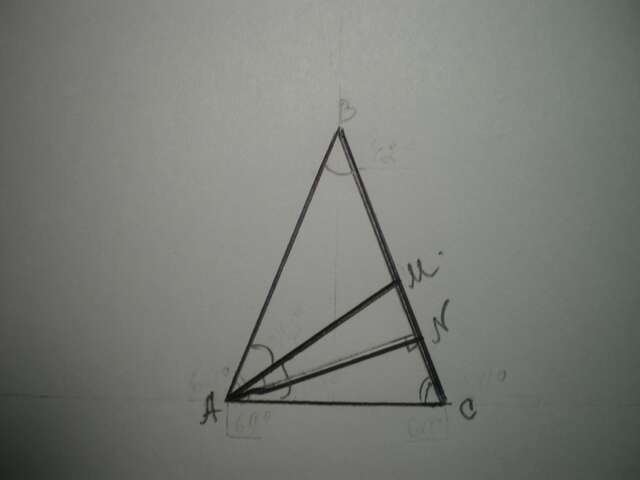
Дано: ΔАВС, АВ=ВС, ∡В=22°, АN - высота, АM - биссектриса. Найти ∡MАN.
В равнобедренном треугольнике углы при основании равны, поэтому ∠С=∠ВАС=(180-22):2=79°
ΔСАN - прямоугольный, ∠СNА=90°, ∠NАС=90-79=11°, т.к. сумма острых углов прямоугольного треугольника составляет 90°.
∡MАС=1/2 ∡ВАС=79:2=39,5°
∡MАN=39,5-11=28,5°