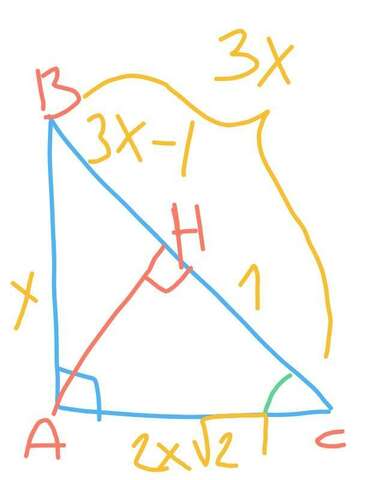Проекция одного из катетов на гипотенузу равна 1 см.А синус одного из острых углов...

Пусть НС - проекция катета АС на гипотенузу ВС и равна 1 см. Пусть синус угла С равен 1/3 (АВ/ВС). Тогда пусть АВ = х и ВС = 3 х. Следовательно, ВН = 3х - 1 см. По теореме Пифагора АС^2 = ВС^2-АВ^2 ; АС^2 = 9х^2-х^2 ; АС^2 = 8х^2 ; АС = х√8 ; АС = 2х√2.

Проекции катетов на гипотенузу относятся как квадраты катетов.

Тоесть, ВН/НС = АВ^2/АС^2 ; 3х-1 = х^2/8х^2

$8x {}^{2} (3x - 1) = x {}^{2} \\ 8(3x - 1) = 1 \\ 24x - 8 - 1 = 0 \\ 24x - 9 = 0 \\ x = 0.375$

Ответ : 0,375 см

Проекция одного из катетов ** гипотенузу равна 1 см.А синус одного из острых углов...