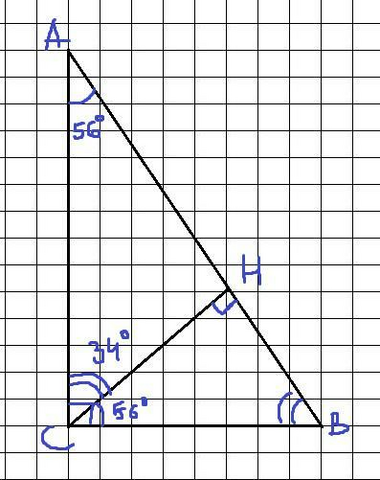
Ответ:
Угол с меньшим катетом равен 34°;
Угол с большим катетом равен 56°.
Объяснение:
1)Рассмотрим ΔABC:
∠A = 56°; ∠C = 90°; ∠B = 90° - ∠A ⇒ ∠B = 90° - 56° = 34°
2) Рассмотрим ΔAHC:
∠HAC = 56°; ∠CHA = 90°; ∠ACH = 90° - 56° = 34°
3) Рассмотрим ΔHCB:
∠HBC = 34°; ∠BHC = 90°; ∠HCB = 90° - 34° = 56°
4) Так как мы знаем, что против бОльшего угла лежит бОльший катет, то катет CB, лежащий против ∠A = 56° - больше, чем катет AC. Следовательно, угол с меньшим катетом равен 34°; угол с бОльшим катетом равен 56°