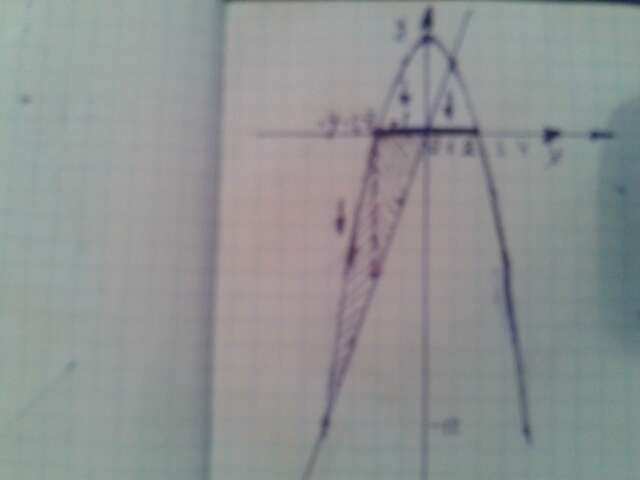
Ответ: S=13,333 кв.ед.
Пошаговое объяснение:
y=4-x² y=3x y=0 S=?
4-x²=3x
x²+3x-4=0 D=25 √D=5
x₁=-4 x₂=1.
4-x²=0
x²=4
x₁=-2 x₂=2.
3x=0 |÷3
x=0.
S=S₁+S₂+S₃
S₁=₋₄∫⁻²(4-x²-3x)dx=4x-(x³/3)-(3x²/2) ₋₄|⁻²=
=4*(-2)-((-2)³/3)-1,5*(-2)²-(4*(-4)-((-4)³*3)-1,5*(-4)²)=-8+(8/3)-6-(-16+(64/3)-24)=
=-14+2²/₃-(21¹/₃-40)=-11¹/₃-(-18²/₃)=-11¹/₃+18²/₃=7¹/₃.
S₂=₋₂∫⁰(0-3x)dx=-3x²/2 ₋₂|⁰=-1,5x² ₋₂|⁰=-1,5*0²-(-1,5*(-2)²)=0-(-6)=6.
S₃=₀∫²0dx=0*₀∫²dx=0.
S=7¹/₃+6+0=13¹/₃.