Задача 4. Докажите, что биссектрисы внутренних односторонних углов при параллельных...

Question

Задача 4. Докажите, что биссектрисы внутренних односторонних углов при параллельных прямых и секущей взаимно перпендикулярны. Дано: а || b, AК — биссектриса; ВК — биссектриса. Доказать: ∠AKB = 90°.

Answer 1

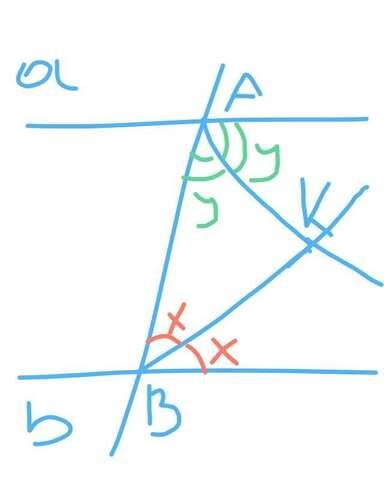
Пусть угол АВК = х и угол ВАК = у. Тогда угол А = 2у, а угол В = 2х. Так как они односторонние при параллельных прямых, то 2х+2у=180°.

2(х+у)=180° | : 2

х+у=90°

Угол АКВ = 180°-(х+у)= 180°-90° = 90°. (Если сумма двух углов треугольника равна 90°, то треугольник прямоугольный)

Ответ : что требовалось доказать.

---