Ответ:
∠АВМ = 60°.
Объяснение:
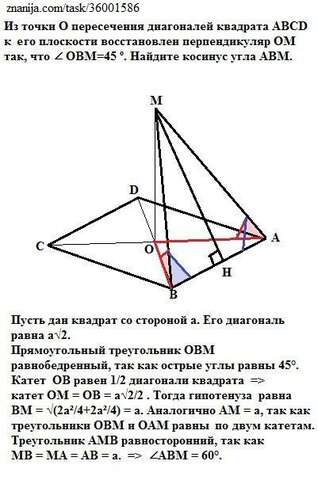
Пусть дан квадрат со стороной а. Его диагональ равна а√2.
Прямоугольный треугольник ОВМ равнобедренный, так как острые углы равны 45°.
Катет ОВ равен 1/2 диагонали квадрата =>
катет ОМ = ОВ = а√2/2 . Тогда гипотенуза равна
ВМ = √(2а²/4+2а²/4) = а.
Аналогично АМ = а, так как треугольники ОВМ и ОАМ равны по двум катетам. Треугольник АМВ равносторонний, так как
МВ = МА = АВ = а. => ∠АВМ = 60°.