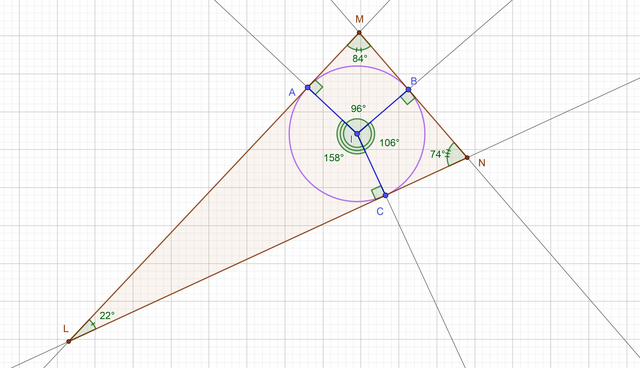
Дуга равна соответственному центральному углу.
∪CA = 360°−∪AB−∪BC = 360−96−106 = 158°
I — центр вписанной окружности в треугольник; IA = IB = IC — радиусы.
∢AIC = ∪CA = 158°; ∢AIB = ∪AB = 96°; ∢BIC = ∪BC = 106°
IA ⊥ LM, IB ⊥ MN, IC ⊥ NL (радиус ⊥ к касательной)
∢IAM = ∢MBI = ∢IBN = ∢NCI = ∢ICL = ∢LAI = 90°
∢L= 360°−∢AIC−∢LAI−∢ICL = 360−158−90−90 = 360−180−158 =180(2-1)-158=180-158 = 22° (из 4-угольника AICL)
аналогично для других углов:
∢ M= 180−96 = 84°
∢ N= 180−106 = 74°
Ответ:
- ∢L= 22°
- ∢M = 84°
- ∢N = 74°
- ∪CA = 158°