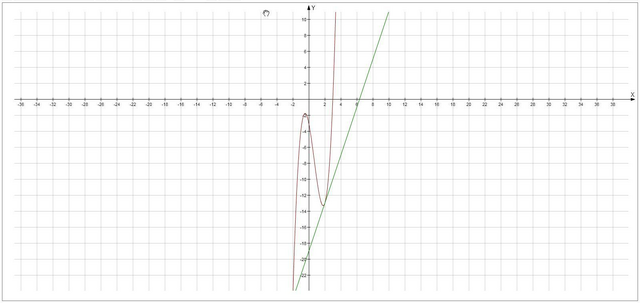
Задача: Найти уравнение касательной к графику функции f(x)=2x³−4x²−5x−3 в точке x₀=2.
Решение:
Уравнение касательной к графику функции f(x) в точке x=a находится по формуле:
y = f(a)+f′(a)⋅(x−a)
Сначала найдём производную функции f(x):
f′(x) = 6x²−8x−5
Затем найдём значение функции и её производной в точке a:
f(a) = f(2) = −13
f′(a) = f′(2) = 3
Подставим числа a = 2; f(a) = −13; f′(a) = 3 в начальную формулу:
y =−13+3(x−2) = 3x−19
Ответ: y=3x−19.