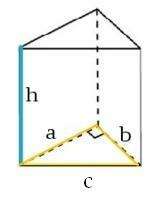
Обозначим стороны треугольника за a = 30 см, b = 40 см, c — гипотенуза. Обозначим высоту призмы за h.
Найдем гипотенузу прямого треугольника за т. Пифагора:

Боковая грань прямой призмы — прямоугольник. Большая грань призмы со сторонами c и h.
Используя формулу площади прямоугольника, найдем вторую сторону h, которая и является высотой призмы.

Ответ: Высота призмы равна 6 см.