В остроугольном треугольнике ABC провели высоту BH, биссектрису BL и медиану BM (H лежит...

Question

В остроугольном треугольнике ABC провели высоту BH, биссектрису BL и медиану BM (H лежит между A и L). Оказалось, что AH=HL=LM. Найдите AC^2:BC^2

Answer 1

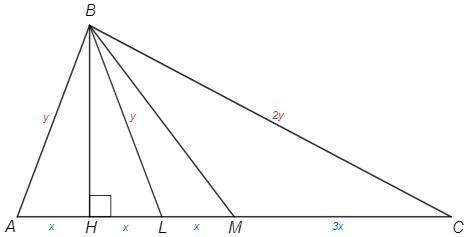
Взаимное расположение высоты, биссектрисы, медианы.

BH

AH=HL, BH - высота и медиана => ABL - равнобедренный, AB=BL

AH=HL=LM=x, AM=MC=3x

AB/BC =AL/LC =2x/4x =1/2 (теорема о биссектрисе)  

AB=BL=y, BC=2y

BL^2 =AB*BC -AL*LC (формула биссектрисы)

y^2 =2y^2 -8x^2 => x^2/y^2 =1/8

AC^2/BC^2 =(6x)^2/(2y)^2 =36/4 *1/8 =9/8

---