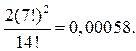Відповідь:
а) Пусть событие А – никакие два лица одного пола не сядут рядом. Общее число способов рассадки 14 лиц на 14 местах определяется числом перестановок n = Р14 = 14!. Если женщины займут чётные места 7! способами, то мужчины будут занимать нечётные места также 7! способами и наоборот, т.е. число случаев, благоприятствующих событию А равно m1 = 2 ∙ ( 7! )2. Поэтому справедливо
р(А) = m1/n = 0,00058
б) Пусть событие В – мужчины и женщины (7 пар) сядут рядом. В этом случае число исходов m2, благоприятствующих событию В определяется числом 7! всевозможных перестановок 7 пар, причём в каждой паре возможна перестановка мужчины и женщины; по правилу произведения m2 = 7! ∙ 27 . Будем иметь
р(В) = m2/n = 0,0000074
Покрокове пояснення: