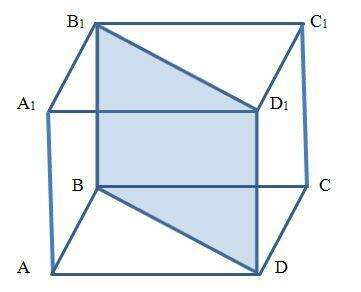
Ответ:
80√2
Объяснение:
Sbb1d1d=110
DD1=11
так как в диагональное сечение прямоугольник, то ВD= S/DD1=110/11=10
Диагональ квадрата создает внутри него равнобедренный прямоугольный треугольник скатетами в виде его сторон и диагональю, как гипотенузой, из чего можно вывести следующуютеорему Пифагора:
a^2+a^2=d^2
2a^2=d^2a=√d^2/2=√10^2/2=√50 =AB=AD
Sбок= a*h+a*h+a*h+a*h=4a*h= 4*√50*10=40*√50=40*5√2=80√2