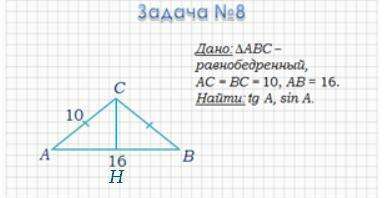
Задача: Дан ΔABC — равнобедренный, AC = BC = 10, AB = 16. Найти tg A, sin A.
Решение:
Проведем высоту CH в ΔABC к стороне AB. Образуется два равных треугольника, т.к. ΔABC равнобедренный. AH = HB = 16/2 = 8.
Р-м ΔACH:
∠AHC = 90°, т.к CH — перпендикуляр к AH (AH∈AB) ⇒ ΔACH — прямоугольный.
Синус угла равен отношению противолежащего катета к гипотенузе.
Найдем катет CH за т. Пифагора:

Тогда синус ∠A будет равен:

Тангенс угла равен отношению противолежащего катета к прилежащему:

Ответ: tg A = 0,75; sin A = 0,6.