Ответ: S=0,5.
Пошаговое объяснение:
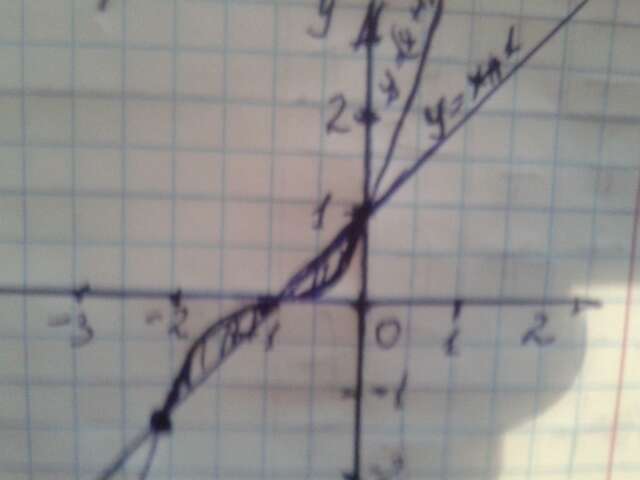
y=y+1 y=(x+1)³ S=?
x+1=(x+1)³
(x+1)³-(x+1)=0
(x+1)*((x+1)²-1)=0
(x+1)*(x+1+1)*(x+1-1)=0
(x+1)*(x+2)*x=0
x₁=-2 x₂=-1 x₃=0
S=S₁+S₂
S₁=₋₂∫⁻¹((x+1)³-(x+1))dx=₋₂∫⁻¹(x+3)³dx-₋₂∫⁻¹(x+1)dx
S₂=₋₁∫⁰((x+1)-(x+3)³)dx=₋₁∫⁰(x+1)dx-₋₁∫⁰(x+1)³dx
∫(x+1)³dx
Пусть x+1=u ⇒ d(x+1)=dx=du ⇒ ∫(x+1)³dx=∫u³du=u⁴/4=(x+1)⁴/4.
∫(x+1)dx
Пусть x+1=u ⇒ d(x+1)=dx=du ⇒ ∫(x+1)dx=∫udu=u²/2.
S₁=(x+1)⁴/4-(x+1)²/2 -₂|⁻¹=(-1+1)⁴/4-(-1+1)²/2-((-2+1)⁴/4-(-2+1)²/2))=
=0⁴/4-0²/2-((-1)⁴/4-(-1)²/2)=0-(1/4-1/2)=-(-1/4)=1/4=0,25.
S₂=(x+1)²/2-(x+1)⁴/4) ₋₁|⁰=(0+1)²/2-(0+1)²/2-((-1+1)²/2-(-1+1)⁴/4))=
=(1/2-(1/4)-(0²/2-0⁴/4)=(1/4)-0=1/4=0,25.
S=S₁+S₂=0,25+0,25=0,5.