Объяснение:
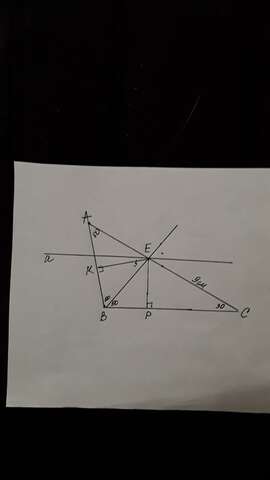
ΔABC, ∠А=50,∠В=30,ВЕ-биссектриса Е⊂а, а║ВС, ЕС=9 см.
Найти: а) Расстояние между прямыми а и BC б) Расстояние от точки Е до прямой AB
Решение.
а)ΔАВС , ∠С=180°-100°-50°=30°.
Пусть ЕР⊥ВС, тогда ЕР-расстояние от точки Е до прямой ВС.
ΔЕРС-прямоугольный. По свойству угла 30° имеем ЕР=1/2ЕС, ЕР=4,5 см.
б)Пусть ЕК⊥АВ, тогда ЕК-расстояние от точки Е до прямой AB. Точки К и Р лежат на сторонах угла ∠АВС, ВЕ-биссектриса и значит
каждая точка биссектрисы неразвернутого угла равноудалена от сторон угла⇒ЕК=ЕР=4,5 см.