Объяснение:
1)
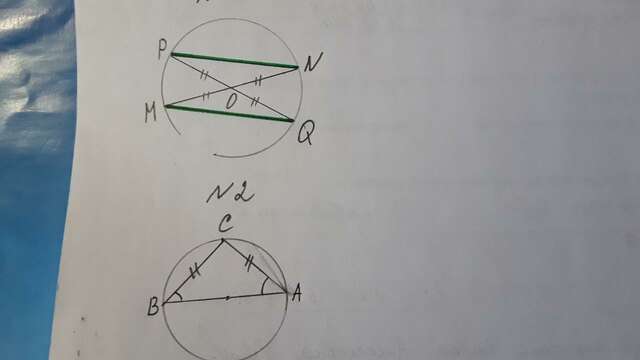
Пусть О-центр окружности.
Тогда ΔОMQ=ΔОNР по 2-м сторонам и углу между ними :MО=ОN как радиусы,ОQ=ОP как радиусы, ∠MОQ=∠NОР как вертикальный .В равных треугольниках соответственные элементы равны: MQ=NР .
2)
ΔАВС. Точка О-центр окружности ⇒ОА=ОВ.
ΔАОС=ΔВОС по трем сторонам :
ОА=ОВ (см. выше),
СА=СВ по условию,
СО-общая. В равных треугольниках соответственные элементы равны: ∠А=∠В.