Ответ:
А) ∠КМО = 30°
Б) ∠КМО = 45°
Объяснение:
1) Радиус окружности, проведённый из центра О к касательной в точку К, всегда составляет прямой угол с этой касательной.
То есть ∠OKM = 90°, а следовательно получившийся в результате построения треугольник ΔOKM - прямоугольный.
2(а)
По условию:
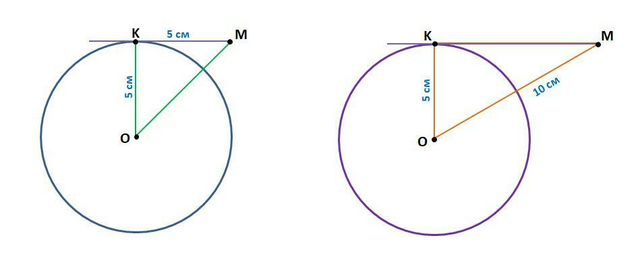
Радиус ОК = 5 см – катет противолежащий углу М (∠КМО)
ОМ = 10 см - гипотенуза
Синус угла - отношение противолежащего этому углу катета к гипотенузе:
sin(α)=a/c ; sin(M) = OK/OM = 5/10 = ½ , sin(½) = 30°
2(б)
По условию:
Радиус ОК = 5 см – катет противолежащий углу М
Касательная МК = 5 см - катет прилежащий углу М
Тангенс угла - отношение противолежащего катета к прилежащему:
tg(α)=a/b ; tg(Μ) = ОК/МК = 5/5 = 1, tg(1) = 45°