Ответ:
180 см². 18√3 см².
Объяснение:
1.
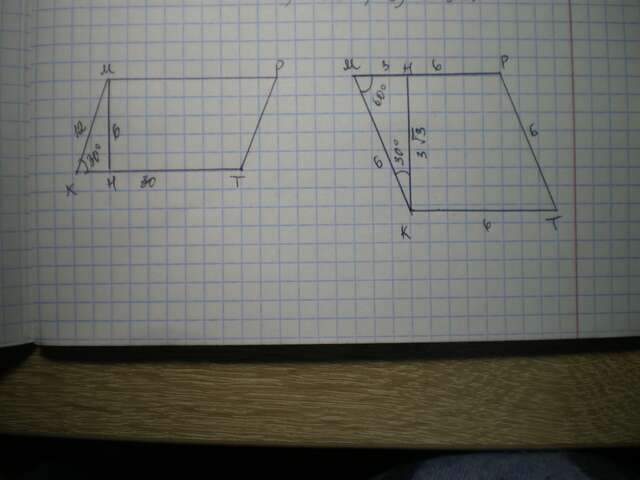
Дано: КМРТ - параллелограмм, ∠К=30°, КМ=12 см, КТ=30 см. Найти S(КМРТ).
S=a*h
Проведем высоту МН, имеем ΔКМН; МН лежит против угла 30°, значит МН=1/2 КМ=12:2=6 см.
S=КТ*МН=30*6=180 см².
2.
Дано: КМРТ - ромб, ∠М=60°, КМ=МР=РТ=КТ=6 см. Найти S(КМРТ).
S=a*h.
Проведем высоту КН, имеем ΔКМН; МН лежит против угла 30°, значит МН=1/2 КМ=6:2=3 см.
По теореме Пифагора КН=√(КМ²-МН²)=√(36-9)=√27=3√3 см
S=КН*МР=3√3 * 6 = 18√3 см².