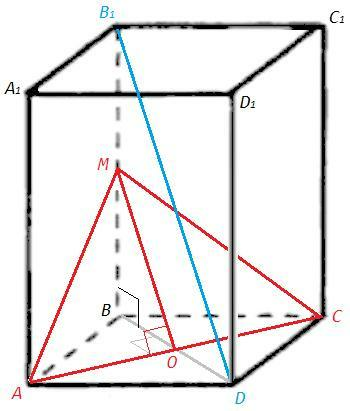
Правильная четырехугольная призма - прямая (боковые рёбра перпендикулярны основаниям), в основаниях квадраты.
Диагонали квадрата перпендикулярны, равны, точкой пересечения делятся пополам.
AC⊥BD, BO=OD
MO - средняя линия в треугольнике B1BD
MO||B1D, MO=B1D/2
Диагональ B1D параллельна прямой MO в плоскости (AMC), следовательно параллельна самой плоскости.
Треугольник AMC - данное сечение.
S(AMC) =5√6
BO - проекция наклонной MO, BO⊥AC => MO⊥AC (теорема о трех перпендикулярах)
S(AMC) =1/2 AC*MO => MO =2 *5√6 /2√5 =√30
B1D =2MO =2√30