Ответ:
2 см, 32 см, 136 см²
Объяснение:
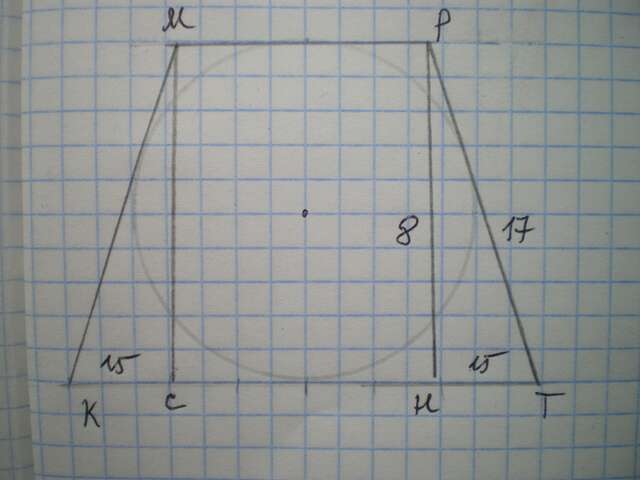
Если вокруг трапеции можно описать окружность, значит сумма боковых сторон равна сумме оснований трапеции. По условию КМ=РТ=17 см, КМ+РТ=МР+КТ=17+17=34 см.. Высота РН=D=8 см
S=(КМ+РТ):2*РН=34:2*8=136 см²
Проведем высоту МС=РН=8 см.
ΔКМС=ΔТРН по катету и гипотенузе, поэтому КС=ТН
Найдем ТН по теореме Пифагора
ТН=√(РТ²-РН²)=√(289-64)=√225=15 см.
КС+ТН=15+15=30 см
Пусть МР=х см, тогда КТ=х+30 см
х+х+30=34; 2х+30=34; 2х=4; х=2.
МР=2 см, КТ=2+30=32 см.