Ответ:
7
Пошаговое объяснение:
1) Думаю самое быстрое решение - это графический метод:
строим графики функций по точкам
![y=\sqrt[3]{4x-1} \\ y=\sqrt[3]{x+1} +1 y=\sqrt[3]{4x-1} \\ y=\sqrt[3]{x+1} +1](https://tex.z-dn.net/?f=y%3D%5Csqrt%5B3%5D%7B4x-1%7D%20%20%5C%5C%20y%3D%5Csqrt%5B3%5D%7Bx%2B1%7D%20%2B1)
они пересекаются в точке с абсциссой x=7, что и будет ответом.
2) Но если нужно аналитическое решение, то вот одно из них
сделаем замену:
![\sqrt[3]{x+1} =t \sqrt[3]{x+1} =t](https://tex.z-dn.net/?f=%5Csqrt%5B3%5D%7Bx%2B1%7D%20%3Dt)
тогда

имеем уравнение:
![\sqrt[3]{4(t^3-1)-1} -t=1 \\ \\ \sqrt[3]{4t^3-5} =t+1 \sqrt[3]{4(t^3-1)-1} -t=1 \\ \\ \sqrt[3]{4t^3-5} =t+1](https://tex.z-dn.net/?f=%5Csqrt%5B3%5D%7B4%28t%5E3-1%29-1%7D%20-t%3D1%20%5C%5C%20%5C%5C%20%5Csqrt%5B3%5D%7B4t%5E3-5%7D%20%3Dt%2B1)
возводим обе части в куб:

если данное уравнение имеет целые корни, то они среди делителей свободного члена (-2)
То есть возможные корни: ±1; ±2
перебирая их, выясняем, что подходит только t=2.
Действительно, 2³-2²-2-2=0
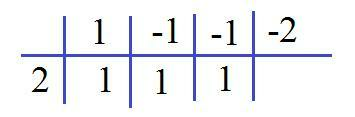
Далее понижаем степень уравнения, например, по схеме Горнера (см. рисунок)
t²+t+1=0
D=1-4=-3<0 ⇒ корней нет</p>
Получается единственный корень t=2
Обратная замена: ∛(x+1)=t
![\sqrt[3]{x+1}=2 \\ \\ (\sqrt[3]{x+1})^3=2^3 \\ \\ x+1=8 \\ \\ x=7 \sqrt[3]{x+1}=2 \\ \\ (\sqrt[3]{x+1})^3=2^3 \\ \\ x+1=8 \\ \\ x=7](https://tex.z-dn.net/?f=%5Csqrt%5B3%5D%7Bx%2B1%7D%3D2%20%5C%5C%20%5C%5C%20%20%28%5Csqrt%5B3%5D%7Bx%2B1%7D%29%5E3%3D2%5E3%20%5C%5C%20%5C%5C%20x%2B1%3D8%20%5C%5C%20%5C%5C%20x%3D7)