Ответ:
V фигуры = 224π см³ ≈ 703 см³
Пошаговое объяснение:
Данную фигуру можно разделить на цилинд и конус.
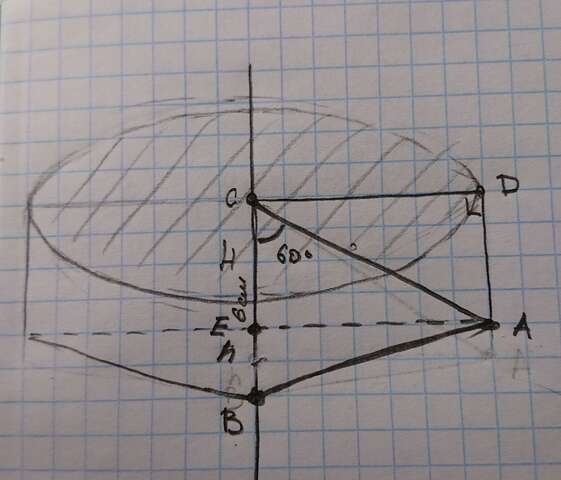
Проведём высоту треугольника ABC из угла A к основанию BC. Пересечение с BC отметим как точку E (см рисунок)
Тогда прямоугольник ACED при вращении образует цилиндр, а треугольник ABE - конус
Радуиусы фигур будут одинаковыми
R = 8*Sin 60° = 8*√3/2 = 4*√3 см
Высота цилиндра H = 8*Cos 60° = 8*1/2 = 4 см
Высота конуса h = CB - h = 6 - 4 = 2 см
V цилиндра = π*R²*H = π * 4² *3*4 = 192π см³
V конуса = 1/3π*R²*h = π * (1/3) * 4² * 3 * 2 = 32π см³
V фигуры = Vц + Vк = 224π см³ ≈ 703 см³