Дано: Окр.(О;3см), МК – касательная, ОМ = ОК = 5см. Найти: МК.

Question

Дано: Окр.(О;3см), МК – касательная, ОМ = ОК = 5см. Найти: МК.

Answer 1

Ответ:

8 см

Пошаговое объяснение:

Обозначим точку касания Н.

Радиус, проведенный в точку касания, перпендикулярен касательной (свойство).  =>

⊿ МОН и⊿ КОН прямоугольные и равны по равным гипотенузам МО=ОК=5 см (дано) и общему катету ОН=3 см. Эти треугольники «египетские», второй катет МН=КН=4 см.

Поэтому МК=МН+КН=8 см.

Answer 2

Ответ:

8 см

Пошаговое объяснение:

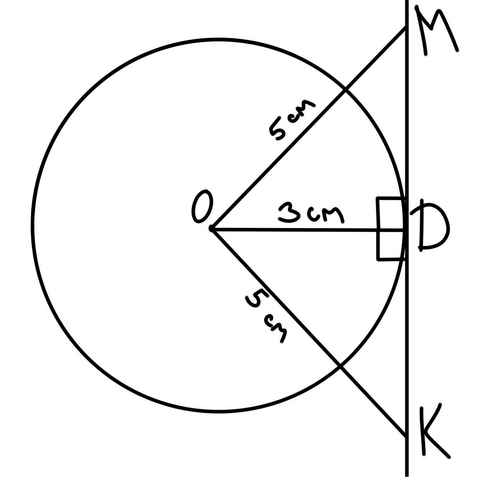
Итак, там известно, что радиус у окружности О = 3 см, касательная пересекает всегда окружность только в 1 точке, назовем ее D. Касательная - это прямая, которая при пересечении с радиусом дает угол в 90 градусов. Если ОМ=ОК=5 см, то у нас образуется 2 прямоугольных треугольника: ОMD и OKD, в которых MD+DK=MK, а значит найдя MD и DK мы сможем найти ответ.

Найдем стороны через Теорему Пифагора: a²+b²=c²

a и b в прямоугольном треугольнике - это катеты, но у нас известен 1 катет и гипотенуза, а значит наша формула будет выглядеть вот так:

3²+b²=5²

Теперь просто решаем самое простое уравнение:

3²+b²=5²

9+b²=25

b²=25-9

b²=16

= 4 см

Теперь просто умножаем на 2: 4×2=8 см

Попыталась как можно подробнее объяснить :з

---