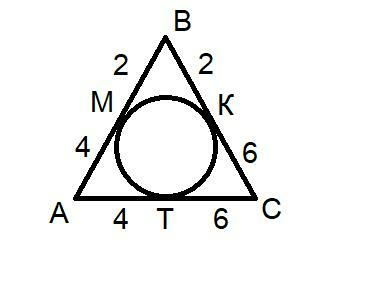Нужно с дано и рисунком : 1. В треугольник вписана окружность так, что три из шести...

Question

Нужно с дано и рисунком : 1. В треугольник вписана окружность так, что три из шести получившихся отрезков касательных равны 2см, 4см, 6см. Найдите периметр треугольника. 2. Хорды АВ и СD пересекаются в точке Е так, что АЕ=3см, ВЕ=36 см, СЕ:DE=3:4. Найдите величину хорды CD. 3. Точки А и В делят окружность с центром О на дуги АМВ и АСВ так, что дуга АСВ на 80 0 меньше дуги АМВ, АМ – диаметр окружности. Найдите величины углов АМВ, АВМ, АСВ.

Answer 1

Задача 1 (рисунок 1).

1) МВ и КВ, МА и ТА, КС и ТС - отрезки касательных, проведённых из одной точки. Они равны по свойству касательных. Следовательно, треугольник АВС разбивается на три пары равных (попарно) отрезков.

PΔАВС=2*2+4*2+6*2=24см.

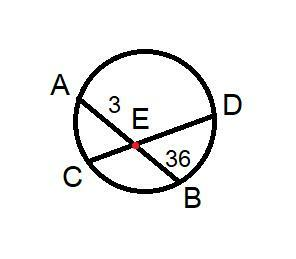
Задача 2 (рисунок 2).

3:4=3х+4х

По теореме о пересекающихся хордах:

36*3=3х*4х

108=12х²

х=3.

CD=3*7=21см.

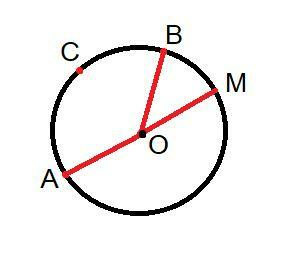
Задача 3 (рисунок 3).

Сначала ищем градусную меру дуг АМВ и АСВ.

Если 2 дуги, на которые делит окружность любая хорда, вместе равны 360°, то:

(360-80):2=140° - дуга АСВ.

Тогда дуга АМВ = 140+80=220°. (в сумме 360).

Дальше пользуемся свойствами вписанных и центральных углов:

1) ∠АСВ=150°, ∠АОВ=210° (центральные ∠).

2) ∠АМВ=половине АОВ=75°, ∠АВМ=половине АОМ=90°,

3)∠АСВ=половине АМВ=105° (вписанные углы).

Ответ: 210° - ∠АМВ, 90° - ∠АВМ, 105° - ∠АСВ.

---

---

---

Comments

1 задача. Дано: вписанная окружность, три точки касания. 3/6 отрезков = соответственно 2, 4 и 6см. Найти: периметр АВС.

---

2 задача: пересекающиеся в точке Е хорды АВ, СD. АЕ=3, ЕВ=36. СЕ:ЕD=3:4. Найти: CD.

---

3 задача: точки А и В принадлежат окружности с центром в точке О. Дуга АСВ на 80 градусов меньше дуги АМВ. АМ - диаметр. Найти: углы АМВ, АВМ и АСВ.

---

Готово)

---

Огромное спасибо