Ответ: 10 и 10√2
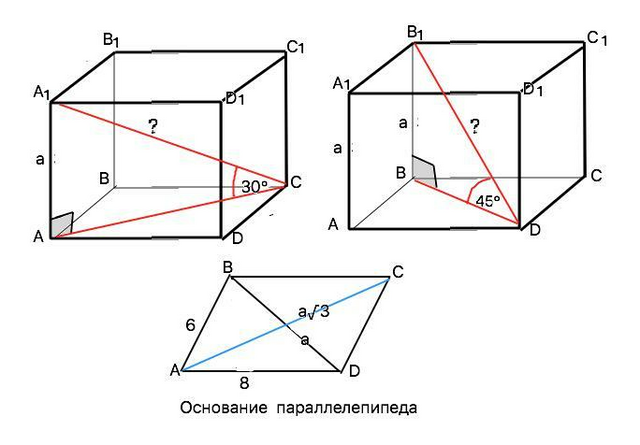
Объяснение: Параллелепипед АВСDD1А1В1С1 – прямой, ⇒ боковые ребра перпендикулярны основаниям.
Примем боковое ребро равным а.
Диагональ В1D наклонена к плоскости основания под углом 45°⇒ ∠В1DВ=45°, В1D=а:sin45°=a√2
A1C наклонена к плоскости АВСD под ∠30° ⇒ АС=а:tg30°=a√3
В основании параллелепипеда - параллелограмм. В параллелограмме сумма квадратов диагоналей равна сумме квадратов всех его сторон:
2•6*+2•8²=а²+3а² ⇒
4а²=200 ⇒ а=5√2
Тогда В1D=а√2=5√2•√2=10
A1C=AA1:sin30°=5√2…1/2=10√2